难度困难185收藏分享切换为英文接收动态反馈
这个问题和“最多能完成排序的块”相似,但给定数组中的元素可以重复,输入数组最大长度为2000,其中的元素最大为10**8。
arr是一个可能包含重复元素的整数数组,我们将这个数组分割成几个“块”,并将这些块分别进行排序。之后再连接起来,使得连接的结果和按升序排序后的原数组相同。
我们最多能将数组分成多少块?
示例 1:
输入: arr = [5,4,3,2,1]
输出: 1
解释:
将数组分成2块或者更多块,都无法得到所需的结果。
例如,分成 [5, 4], [3, 2, 1] 的结果是 [4, 5, 1, 2, 3],这不是有序的数组。
示例 2:
输入: arr = [2,1,3,4,4]
输出: 4
解释:
我们可以把它分成两块,例如 [2, 1], [3, 4, 4]。
然而,分成 [2, 1], [3], [4], [4] 可以得到最多的块数。
注意:
arr的长度在[1, 2000]之间。arr[i]的大小在[0, 10**8]之间。
解析
根据题目的意思可能明确知道,尽量分块使得最后能分块的个数最多。是一个最值问题,那么就可以使用贪心算法,也就是使得每一个分块的窗口最小。
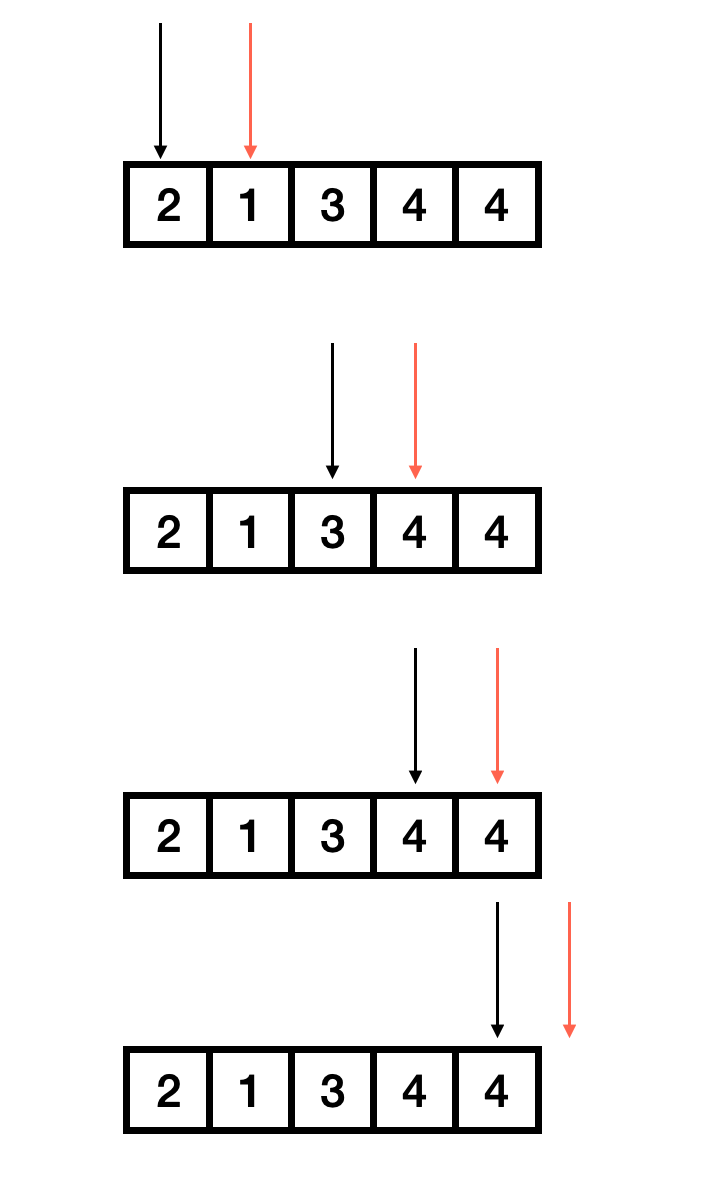
其实每一次窗口的左边界是确定的(上一次的右边界值),代表的是左闭右开,我们需要确定的是最小的右边界。
这时候通过模拟发现:
某一段能否成为区间是取决于后面的元素,也就是说,区间后面的元素都要 <= 区间内的最大值
/*
加入可能不能分块的情况,也就是说,分块的排序最后与整体的排序一致
设计数据结构
std:::map> data
第一层索引代表的是数字
第二层索引代表的是位置
*/
#include
#include 由于处理结果取决与后面元素的分布情况,适用于栈的处理方式
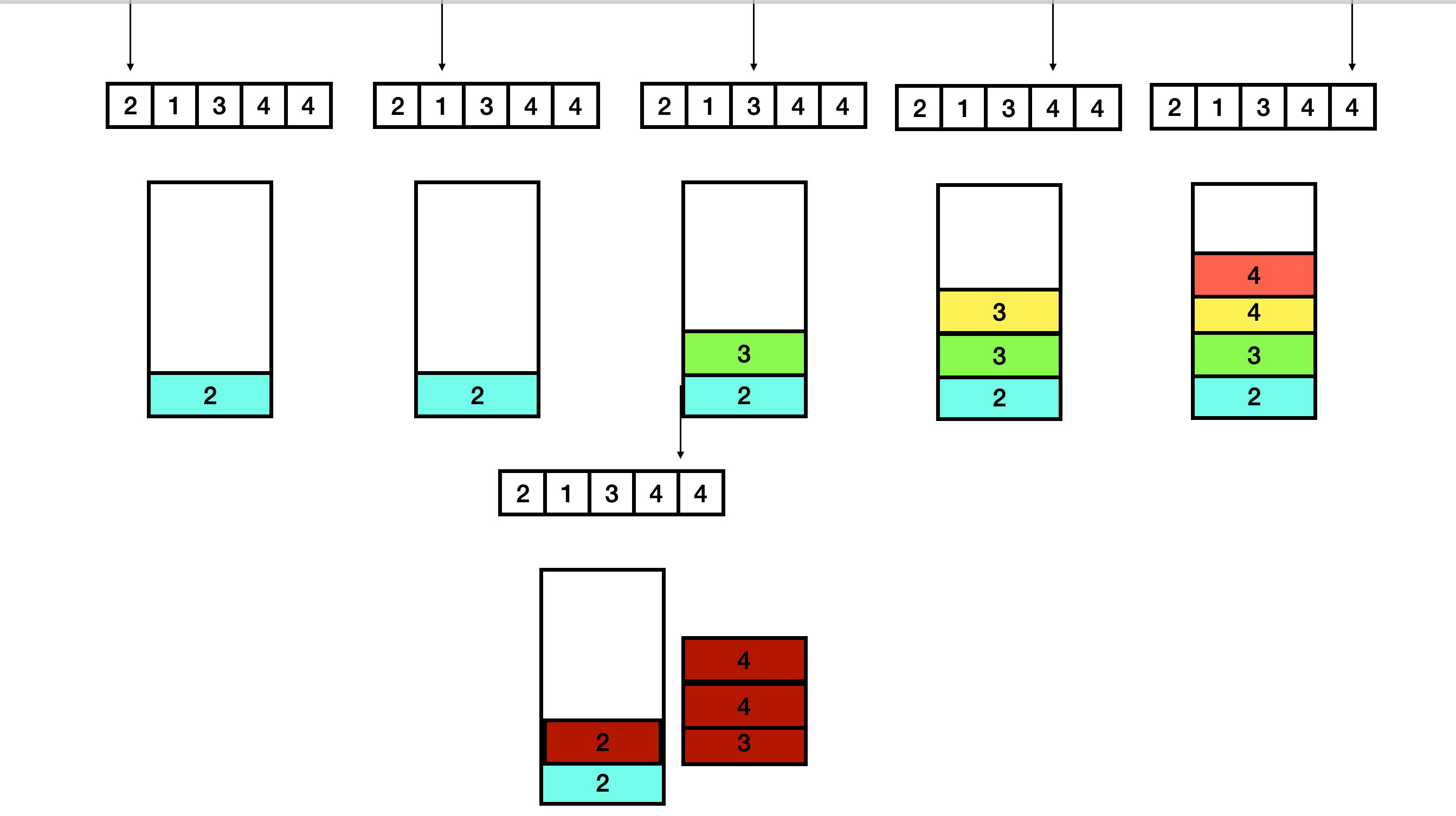
栈内每一个色块代表的是可能成为的一个组,值代表组内的最大值;当后面有值小于当前的最大值的时候就需要合并。最终的思想就是后面的元素都大于等于当前块内的最大值。
class Solution {
public:
stack _st;
int maxChunksToSorted(vector& arr) {
for(auto& val : arr) {
if(_st.empty()) {
_st.push(val);
} else {
if(_st.top() <= val) { _st.push(val); } else if(_st.empty()) continue; int tmp_max="_st.top();" while(!_st.empty() && _st.top()> val) {
_st.pop();
}
// 更新最大值
_st.push(tmp_max);
}
}
}
return _st.size();
}
};

